Krzywizna krzywej

Krzywiznę krzywej płaskiej definiuje się jako:

$\kappa=\lim_\Delta S\rightarrow 0\frac\Delta\varphi\Delta S=\fracd\varphidS$

gdzie $\Delta\varphi$ jest kątem pomiędzy stycznymi do krzywej na końcach łuku, a 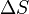$\Delta S$ długością tego łuku.

Krzywizna okręgu jest w każdym punkcie jednakowa i równa odwrotności jego promienia.

Wzory na krzywiznę $\kappa$ w punkcie $P(x_0,y_0)$ są następujące:

Dla krzywej określonej funkcją $y = f(x)$ w układzie kartezjańskim:

$\kappa=\fracy ''_0(1+y'_0^2)^3/2$

Dla krzywej określonej parametrycznie $x = p(t), y = q(t)$ w układzie kartezjańskim:

$\kappa=\fracy''_0x'_0-x''_0y'_0(x'_0^2+y'_0^2)^3/2$

Dla krzywej określonej funkcją $r = f(\varphi)$ w układzie biegunowym:

$\kappa=\fracr_0^2 + 2r'_0^2 - r_0r''_0(r_0^2 + r'_0^2)^3/2$

Promieniem krzywizny krzywej w danym punkcie P nazywamy bezwzględną wartość odwrotności jej krzywizny w tym punkcie, obliczonym jednym ze wzorów podanych powyżej:

$\delta = \left| \frac1\kappa \right|$

Środkiem krzywizny krzywej w danym punkcie $P(x_0,y_0)$ nazywamy punkt $S(\xi,\eta)$ , leżący na normalnej do krzywej w punkcie P po stronie jej wklęsłości w odległości od P równej promieniowi krzywizny.

Wzory na współrzędne środka krzywizny w punkcie P krzywej są następujące:

Dla krzywej o równaniu $y = f(x)$ :

$\xi = x_0-y'_0\frac1+ y'_0^2y''_0, \eta = y_0 + \frac1+y'_0^2y''_0$

Dla krzywej o równaniach $x = p(t), y = q(t)$ :

$\xi = x_0-y'_0\fracx'_0^2 + y'_0^2y''_0x'_0-y'_0x''_0, \eta = y_0+x'_0\fracx'_0^2+y'_0^2y''_0x'_0-y'_0x''_0$

Przykłady

Obliczanie krzywizny krzywej Lissajous opisanej równaniami:

$x(t) = A\sin(at + \delta),\quad y(t) = B\sin(bt).$

Wartości poszczególnych pochodnych:

$x'(t) = Aa\cos(at + \delta)$

$y'(t) = Bb\cos(bt)$

$x''(t) = -Aa^2\sin(at + \delta)$

$y''(t) = -Bb^2\sin(bt)$

Krzywizna jako funkcja parametru t:

$\kappa (t) = \frac -Bb^2\sin(bt) \cdot Aa\cos(at + \delta) + Aa^2\sin(at + \delta) \cdot Bb\cos(bt) \left (A^2a^2\cos^2(at + \delta) + B^2b^2\cos^2(bt) \right )^3/2$

W szczególności dla okręgu $A=B=r,\quad a=b=1,\quad \delta = \frac\pi2$ krzywizna nie zależy od parametru t:

$\kappa (t) = \frac -r\sin(t) \cdot (-r\sin(t)) + r\cos(t) \cdot r\cos(t)\left ( r^2\sin^2(t)+r^2\cos^2(t) \right )^3/2 = \fracr^2r^3=\frac1r$

Natomiast dla elipsy $a=b=1,\quad \delta = \frac\pi2$ krzywizna zależy od parametru t:

$\kappa (t) = \frac -B\sin(t) \cdot (-A\sin(t)) + A\cos(t) \cdot B\cos(t)\left ( A^2\sin^2(t)+B^2\cos^2(t) \right )^3/2 = \fracAB\left ( A^2\sin^2(t)+B^2\cos^2(t) \right )^3/2$
Uwaga

W ogólnym przypadku $A \neq B,\quad a \neq b,\quad \delta \in R$ krzywe Lissajous mają przecięcia (istnieją takie $t_1,t_2 \in R$ , dla których $x(t_1) = x(t_2), y(t_1) = y(t_2)$ ).

Zobacz też

łuk zwykły
ewoluta