Podgrupa – w teorii grup zbiór elementów danej grupy, który sam tworzy grupę z działaniem grupy wyjściowej; inaczej podzbiór grupy zamknięty na działanie grupowe i branie odwrotności, który zawiera jej element neutralny (zob. działanie wewnętrzne).
Podgrupy to te z podzbiorów grup, które odzwierciedlają i zachowują ich strukturę algebraiczną; badanie podgrup danej grupy (nazywanej czasem w tym kontekście nadgrupą) dostarcza o niej wielu istotnych informacji umożliwiając głębsze zrozumienie jej budowy. Niekiedy podgrupy wkomponowane są w grupę w szczególny sposób: są niezmiennikami przekształceń algebraicznych (podgrupa normalna, podgrupa charakterystyczna), umożliwiają jednoznaczne przedstawienie elementu grupy jako sumy/iloczynu elementów ich „rozłącznych” podgrup (składnik/czynnik prosty, zob. suma prosta/iloczyn prosty podgrup); w teorii grup przemiennych rozpatruje się podgrupy czyste oraz podgrupy istotne o nieco słabszych, lecz nadal przydatnych, własnościach (przy potencjalnie większej ich liczbie, co ułatwia wskazanie podgrup o lepszych własnościach).
Charakteryzacja
Niech  będzie grupą; podzbiór
będzie grupą; podzbiór  który tworzy grupę ze względu na działanie określone na
który tworzy grupę ze względu na działanie określone na  nazywa się podgrupą grupy
nazywa się podgrupą grupy  i oznacza zwykle
i oznacza zwykle  Dokładniej, podgrupę
Dokładniej, podgrupę 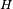 charakteryzują następujące warunki:
charakteryzują następujące warunki:
- Wewnętrzność: działanie grupowe na
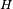 jest zawężeniem działania grupy
jest zawężeniem działania grupy  do zbioru
do zbioru  dlatego iloczyn elementów
dlatego iloczyn elementów  obliczany jest jako iloczyn elementów
obliczany jest jako iloczyn elementów  oraz
oraz  w grupie
w grupie  aby uzyskać dwuargumentowe działanie wewnętrzne na
aby uzyskać dwuargumentowe działanie wewnętrzne na 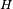 dane wzorem
dane wzorem  tak jak w grupie
tak jak w grupie  potrzeba, a zarazem wystarcza, by
potrzeba, a zarazem wystarcza, by  dla wszystkich
dla wszystkich  Innymi słowy zbiór
Innymi słowy zbiór 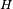 musi być zamknięty ze względu na działanie w
musi być zamknięty ze względu na działanie w 
- Łączność: działanie w
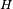 musi być łączne, czyli dla wszystkich
musi być łączne, czyli dla wszystkich  musi zachodzić
musi zachodzić  wiadomo jednak, że
wiadomo jednak, że  dla
dla  a ponieważ
a ponieważ  to powyższy warunek odnosi się w szczególności do elementów
to powyższy warunek odnosi się w szczególności do elementów  w ten sposób łączność działania w
w ten sposób łączność działania w 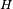 dana jest automatycznie (tzn. wynika wprost z łączności działania w
dana jest automatycznie (tzn. wynika wprost z łączności działania w  ).
). - Element neutralny: zbiór
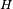 nie może być pusty, gdyż jako grupa
nie może być pusty, gdyż jako grupa 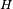 musi mieć element neutralny; niech
musi mieć element neutralny; niech  spełnia
spełnia  dla dowolnego
dla dowolnego  w szczególności dla elementu neutralnego
w szczególności dla elementu neutralnego  grupy
grupy 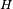 zachodzi
zachodzi  a ponieważ
a ponieważ  to z charakteryzacji elementu neutralnego grupy wynika, że
to z charakteryzacji elementu neutralnego grupy wynika, że  jest elementem neutralnym grupy
jest elementem neutralnym grupy  oznacza to, że element neutralny grupy
oznacza to, że element neutralny grupy  jest zarazem elementem neutralnym w
jest zarazem elementem neutralnym w  o ile tylko należy on do
o ile tylko należy on do  tzn. nie trzeba szukać elementu neutralnego w
tzn. nie trzeba szukać elementu neutralnego w  gdyż jest on niejako z góry – wystarczy tylko sprawdzić, czy element neutralny w
gdyż jest on niejako z góry – wystarczy tylko sprawdzić, czy element neutralny w  należy do
należy do 
- Odwracalność: dla każdego
 musi istnieć
musi istnieć  dla których
dla których  odczytanie tego równania w grupie
odczytanie tego równania w grupie  daje natychmiastowo rozwiązanie
daje natychmiastowo rozwiązanie  w postaci elementu odwrotnego do
w postaci elementu odwrotnego do  w grupie
w grupie  element odwrotny do
element odwrotny do  istnieje w
istnieje w  dlatego nie trzeba go szukać, lecz wystarczy sobie jedynie zapewnić, iż element odwrotny
dlatego nie trzeba go szukać, lecz wystarczy sobie jedynie zapewnić, iż element odwrotny  do
do  należący do
należący do  jest również elementem
jest również elementem 
Podsumowując: niepusty podzbiór 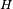 grupy
grupy  jest podgrupą wtedy i tylko wtedy, gdy
jest podgrupą wtedy i tylko wtedy, gdy
- jest zamknięty na działanie:
 dla wszystkich
dla wszystkich 
- zawiera element neutralny:

- jest zamknięty na odwracanie:
 dla każdego
dla każdego 
Co więcej, drugi warunek wynika z pierwszego i trzeciego: niech  (gdyż
(gdyż 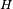 jest niepusty,
jest niepusty,  ), wtedy z trzeciego warunku
), wtedy z trzeciego warunku  a więc
a więc  na mocy pierwszego, co daje
na mocy pierwszego, co daje  Innymi słowy sprawdzenie, czy
Innymi słowy sprawdzenie, czy  można pominąć zakładając, iż
można pominąć zakładając, iż 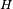 jest niepusty; z drugiej strony jeśli nie wiadomo a priori, czy
jest niepusty; z drugiej strony jeśli nie wiadomo a priori, czy  to najszybszym sposobem zapewnienia tego warunku jest właśnie sprawdzenie, czy
to najszybszym sposobem zapewnienia tego warunku jest właśnie sprawdzenie, czy  Na podstawie powyższych obserwacji można zatem sformułować
Na podstawie powyższych obserwacji można zatem sformułować
- Kryterium bycia podgrupą
- Niepusty podzbiór
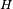 grupy
grupy  jest jej podgrupą wtedy i tylko wtedy, gdy spełnia warunki
jest jej podgrupą wtedy i tylko wtedy, gdy spełnia warunki - oraz
Powyższe dwa warunki (wraz z  ) często łączy się w jeden:
) często łączy się w jeden:  dla wszystkich
dla wszystkich  ; jest on zupełnie równoważny warunkowi
; jest on zupełnie równoważny warunkowi  dla wszystkich
dla wszystkich  . W przypadku skończonym wystarczający jest warunek zamkniętości działania, tzn. prawdziwe jest następujące
. W przypadku skończonym wystarczający jest warunek zamkniętości działania, tzn. prawdziwe jest następujące
- Kryterium bycia podgrupą skończoną
- Niepusty podzbiór skończony
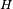 grupy
grupy  bądź niepusty podzbiór
bądź niepusty podzbiór 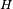 grupy skończonej
grupy skończonej  jest podgrupą wtedy i tylko wtedy, gdy
jest podgrupą wtedy i tylko wtedy, gdy  dla wszystkich
dla wszystkich  .
.
Przykłady
- Podgrupy trywialna i niewłaściwa
- W dowolnej grupie
 zbiór jednoelementowy
zbiór jednoelementowy  oraz zbiór
oraz zbiór  są podgrupami nazywanymi odpowiednio podgrupą trywialną oraz podgrupą niewłaściwą (podgrupy, które nie są trywialne bądź niewłaściwe nazywa się odpowiednio nietrywialnymi oraz właściwymi); jeżeli
są podgrupami nazywanymi odpowiednio podgrupą trywialną oraz podgrupą niewłaściwą (podgrupy, które nie są trywialne bądź niewłaściwe nazywa się odpowiednio nietrywialnymi oraz właściwymi); jeżeli 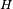 jest podgrupą właściwą w
jest podgrupą właściwą w  to czasem używa się oznaczenia
to czasem używa się oznaczenia  , nietrywialność podgrupy zaznaczana jest osobno. Jeżeli
, nietrywialność podgrupy zaznaczana jest osobno. Jeżeli 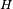 jest podgrupą w
jest podgrupą w  zaś
zaś 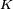 jest podgrupą w
jest podgrupą w  to
to 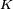 jest podgrupą w
jest podgrupą w 
- Kryterium bycia podgrupą
- Niech
 będzie podzbiorem liczb całkowitych
będzie podzbiorem liczb całkowitych  podzielnych przez
podzielnych przez  Zbiór
Zbiór  tworzy grupę ze względu na dodawanie (wprost z konstrukcji), zaś zbiór
tworzy grupę ze względu na dodawanie (wprost z konstrukcji), zaś zbiór  jest zamknięty ze względu na dodawanie i branie odwrotności, a więc
jest zamknięty ze względu na dodawanie i branie odwrotności, a więc  jest podgrupą w
jest podgrupą w  Analogicznie dowodzi się, że zbiór
Analogicznie dowodzi się, że zbiór  dla dowolnego
dla dowolnego  będącego liczbą naturalną jest podgrupą w
będącego liczbą naturalną jest podgrupą w  a ponadto wszystkie jej podgrupy mają tę postać.
a ponadto wszystkie jej podgrupy mają tę postać.
- Zbiór dodatnich liczb wymiernych tworzy podgrupę
 w grupie
w grupie  niezerowych liczb wymiernych z działaniem mnożenia (iloczyn dowolnych dwóch niezerowych liczb wymiernych dalej jest niezerową liczbą wymierną i podobnie odwrotność niezerowej liczby wymiernej jest niezerową liczbą wymierną), co wynika wprost z własności iloczynu i odwrotności liczb wymiernych: jeśli
niezerowych liczb wymiernych z działaniem mnożenia (iloczyn dowolnych dwóch niezerowych liczb wymiernych dalej jest niezerową liczbą wymierną i podobnie odwrotność niezerowej liczby wymiernej jest niezerową liczbą wymierną), co wynika wprost z własności iloczynu i odwrotności liczb wymiernych: jeśli  to
to  oraz
oraz  podobne obserwacje dotyczą liczb rzeczywistych
podobne obserwacje dotyczą liczb rzeczywistych  (należy wyżej zastąpić
(należy wyżej zastąpić  znakiem
znakiem  i wyraz „wymierny” za pomocą „rzeczywisty”).
i wyraz „wymierny” za pomocą „rzeczywisty”).
- Jeżeli
 są podgrupami w
są podgrupami w  to ich część wspólna
to ich część wspólna  również jest podgrupą w
również jest podgrupą w  Istotnie,
Istotnie,  gdyż
gdyż  oraz
oraz  ponadto jeżeli
ponadto jeżeli  to
to  i
i  skąd
skąd  i
i  a więc
a więc  dodatkowo z
dodatkowo z  wynika
wynika  i
i  a więc
a więc  i
i  co pociąga
co pociąga  stąd
stąd  jest podgrupą w
jest podgrupą w  Analogicznie dowodzi się, że część wspólna
Analogicznie dowodzi się, że część wspólna  rodziny
rodziny  podgrup grupy
podgrup grupy  indeksowanej za pomocą pewnego zbioru indeksów
indeksowanej za pomocą pewnego zbioru indeksów  również jest podgrupą w
również jest podgrupą w 
- Niech
 oznacza zbiór wszystkich wzajemnie jednoznacznych odwzorowań przedziału jednostkowego " src="//upload.wikimedia.org/math/0/8/8/088246d70e0c47595fc9931fcdb11d4c.png"/>liczb rzeczywistych; tworzy on grupę ze względu na składanie odwzorowań (zob. grupa: Przykłady). Zbiór
oznacza zbiór wszystkich wzajemnie jednoznacznych odwzorowań przedziału jednostkowego " src="//upload.wikimedia.org/math/0/8/8/088246d70e0c47595fc9931fcdb11d4c.png"/>liczb rzeczywistych; tworzy on grupę ze względu na składanie odwzorowań (zob. grupa: Przykłady). Zbiór  jest podgrupą w
jest podgrupą w  jako jej niepusty podzbiór zamknięty na składanie i odwracanie funkcji:
jako jej niepusty podzbiór zamknięty na składanie i odwracanie funkcji:- Otóż zbiór
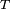 jest niepusty, gdyż należy do niego odwzorowanie tożsamościowe
jest niepusty, gdyż należy do niego odwzorowanie tożsamościowe  dane wzorem
dane wzorem  dla którego zachodzi
dla którego zachodzi 
- Ponadto jeżeli
 to
to  oraz
oraz  co oznacza
co oznacza  a więc
a więc 
- Wreszcie jeśli
 to
to  a zatem
a zatem  stąd
stąd  tzn.
tzn.  czyli
czyli 
- Otóż zbiór
- Kryterium bycia podgrupą skończoną
- Niech dany będzie podzbiór
 grupy
grupy  wraz z mnożeniem modulo
wraz z mnożeniem modulo  przy czym
przy czym  oznacza redukcję liczby całkowitej
oznacza redukcję liczby całkowitej  modulo
modulo  (tzn. resztę z dzielenia
(tzn. resztę z dzielenia  przez
przez  ). Ponieważ
). Ponieważ - to zbiór
 jest zamknięty ze względu na mnożenie. Skoro
jest zamknięty ze względu na mnożenie. Skoro  jest zbiorem skończonym, to na podstawie kryterium bycia podgrupą skończoną zbiór
jest zbiorem skończonym, to na podstawie kryterium bycia podgrupą skończoną zbiór  powinien być podgrupą w
powinien być podgrupą w  Byłaby to prawda, gdyby
Byłaby to prawda, gdyby  była grupą ze względu na mnożenie (nie jest nią, gdyż nie istnieje np. odwrotność elementu
była grupą ze względu na mnożenie (nie jest nią, gdyż nie istnieje np. odwrotność elementu  ); jest ona jednak grupą ze względu na dodawanie, co (jak się okazuje) jest zupełnie czymś innym – aby poprawnie zastosować wspomniane kryterium, należy się więc najpierw upewnić, że nadzbiór tworzy grupę.
); jest ona jednak grupą ze względu na dodawanie, co (jak się okazuje) jest zupełnie czymś innym – aby poprawnie zastosować wspomniane kryterium, należy się więc najpierw upewnić, że nadzbiór tworzy grupę.
- Mimo to
 jest grupą ze względu na mnożenie: z powyższych rozważań wynika, że zbiór ten jest zamknięty na mnożenie, które jest łączne (jest ono w istocie łączne na
jest grupą ze względu na mnożenie: z powyższych rozważań wynika, że zbiór ten jest zamknięty na mnożenie, które jest łączne (jest ono w istocie łączne na  co wynika z własności arytmetyki modularnej); ponadto
co wynika z własności arytmetyki modularnej); ponadto  oraz
oraz  dla wszystkich
dla wszystkich  (z powyższych rozważań lub własności arytmetyki modularnej), skąd
(z powyższych rozważań lub własności arytmetyki modularnej), skąd  jest elementem neutralnym w
jest elementem neutralnym w  każdy element
każdy element  ma odwrotność należącą do
ma odwrotność należącą do  – wynika to z równań
– wynika to z równań 


 oraz
oraz  Korzystając z kryterium bycia podgrupą skończoną można się przekonać, iż podzbiory
Korzystając z kryterium bycia podgrupą skończoną można się przekonać, iż podzbiory 

 są nietrywialnymi podgrupami właściwymi w
są nietrywialnymi podgrupami właściwymi w  gdyż są one zamknięte ze względu na mnożenie (są to jedyne tego rodzaju podgrupy w tej grupie). Podgrupy w
gdyż są one zamknięte ze względu na mnożenie (są to jedyne tego rodzaju podgrupy w tej grupie). Podgrupy w  mają rzędy
mają rzędy  które są dzielnikami rzędu
które są dzielnikami rzędu  grupy
grupy 
- Podzbiór
 tworzy podgrupę grupy
tworzy podgrupę grupy  niezerowych liczb zespolonych względem mnożenia na podstawie kryterium bycia podgrupą skończoną, gdyż jest zamknięta na branie iloczynów. To samo kryterium mówi, że
niezerowych liczb zespolonych względem mnożenia na podstawie kryterium bycia podgrupą skończoną, gdyż jest zamknięta na branie iloczynów. To samo kryterium mówi, że  jest podgrupą w
jest podgrupą w  Ponadto grupa ta nie ma innych nietrywialnych podgrup właściwych, gdyż jeśli podgrupa ta zawierałaby
Ponadto grupa ta nie ma innych nietrywialnych podgrup właściwych, gdyż jeśli podgrupa ta zawierałaby  lub
lub  to musiałaby także zawierać
to musiałaby także zawierać  lub
lub  czyli tworzyłaby wtedy całą grupę
czyli tworzyłaby wtedy całą grupę  Dlatego
Dlatego  ma dokładnie trzy podgrupy: jedną rzędu
ma dokładnie trzy podgrupy: jedną rzędu  jedną rzędu
jedną rzędu  i jedną rzędu
i jedną rzędu  W tym przypadku rzędy podgrup również są dzielnikami rzędu
W tym przypadku rzędy podgrup również są dzielnikami rzędu  grupy
grupy 
- Kryterium może okazać się fałszywe w przypadku, gdy badany podzbiór nie jest skończony: jeśli
 jest podzbiorem dodatnich liczb całkowitych (które można utożsamiać z liczbami naturalnymi
jest podzbiorem dodatnich liczb całkowitych (które można utożsamiać z liczbami naturalnymi  ), to mimo iż
), to mimo iż  jest grupą ze względu na dodawanie, a podzbiór
jest grupą ze względu na dodawanie, a podzbiór 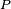 jest zamknięty na to działanie, to nie tworzy on podgrupy, gdyż brak w tym zbiorze elementu neutralnego dodawania (
jest zamknięty na to działanie, to nie tworzy on podgrupy, gdyż brak w tym zbiorze elementu neutralnego dodawania ( ); rozpatrywanie
); rozpatrywanie  (podobnie jak poprzedni przykład) narusza warunek należenia odwrotności (tu: elementu przeciwnego). Grupa
(podobnie jak poprzedni przykład) narusza warunek należenia odwrotności (tu: elementu przeciwnego). Grupa  jest kanonicznym przykładem grupy nieskończonej (wszystkie nieskończone grupy generowane przez jeden element mają tę samą co ona strukturę grupy cyklicznej, zob. izomorfizm).
jest kanonicznym przykładem grupy nieskończonej (wszystkie nieskończone grupy generowane przez jeden element mają tę samą co ona strukturę grupy cyklicznej, zob. izomorfizm).
- Uwagi
- W ogólności suma mnogościowa
 podgrup
podgrup  nie musi być podgrupą: jest tak wtedy i tylko wtedy, gdy
nie musi być podgrupą: jest tak wtedy i tylko wtedy, gdy  bądź
bądź  tzn.
tzn.  lub
lub  czy też
czy też  albo
albo  wynika to z nieco ogólniejszej obserwacji: jeżeli
wynika to z nieco ogólniejszej obserwacji: jeżeli 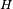 jest podgrupą w
jest podgrupą w  zawartą w
zawartą w  to
to 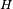 zawiera się w całości w
zawiera się w całości w  lub
lub  (być może w obu z nich). Oznacza to, że nie istnieje grupa, która byłaby sumą mnogościową dwóch swoich nietrywialnych podgrup właściwych; mimo to istnieje grupa, dla której suma jej trzech różnych nietrywialnych podgrup właściwych tworzy w niej podgrupę. Twierdzenie Tomkinsona mówi, iż nie istnieje grupa, którą można zapisać w postaci sumy mnogościowej dokładnie siedmiu jej nietrywialnych podgrup właściwych, z kolei twierdzenie Skorzy stanowi o tym, że jeśli grupa jest sumą trzech nietrywialnych podgrup właściwych, to są one indeksu dwa, a części wspólne dowolnych dwóch z tych trzech podgrup są równe.
(być może w obu z nich). Oznacza to, że nie istnieje grupa, która byłaby sumą mnogościową dwóch swoich nietrywialnych podgrup właściwych; mimo to istnieje grupa, dla której suma jej trzech różnych nietrywialnych podgrup właściwych tworzy w niej podgrupę. Twierdzenie Tomkinsona mówi, iż nie istnieje grupa, którą można zapisać w postaci sumy mnogościowej dokładnie siedmiu jej nietrywialnych podgrup właściwych, z kolei twierdzenie Skorzy stanowi o tym, że jeśli grupa jest sumą trzech nietrywialnych podgrup właściwych, to są one indeksu dwa, a części wspólne dowolnych dwóch z tych trzech podgrup są równe.
- Podgrupę grupy
 generowaną przez jej podzbiór
generowaną przez jej podzbiór  można scharakteryzować jako najmniejszą (w sensie zawierania) podgrupę zawierającą wszystkie elementy zbioru
można scharakteryzować jako najmniejszą (w sensie zawierania) podgrupę zawierającą wszystkie elementy zbioru  tj. część wspólną wszystkich podgrup zawierających zbiór
tj. część wspólną wszystkich podgrup zawierających zbiór  Podgrupę generowaną przez jednoelementowy podzbiór
Podgrupę generowaną przez jednoelementowy podzbiór  grupy
grupy  nazywa się podgrupą cykliczną generowaną przez
nazywa się podgrupą cykliczną generowaną przez  zaś sam element
zaś sam element  nazywa się generatorem tej podgrupy (może mieć ona wiele generatorów); rzędem elementu
nazywa się generatorem tej podgrupy (może mieć ona wiele generatorów); rzędem elementu  nazywa się rząd podgrupy (cyklicznej) generowanej przez ten element, czyli jej liczbę elementów.
nazywa się rząd podgrupy (cyklicznej) generowanej przez ten element, czyli jej liczbę elementów.
- Przypadki grup
 i
i  opisane w wyżej („kryterium bycia grupą skończoną”) sugerują ogólną regułę, iż rząd podgrupy dzieli rząd grupy – w istocie jest ona prawdziwa: rozumowanie w przypadku skończonym wymaga jedynie znajomości pojęć grupy i funkcji (można go znaleźć w rząd: Własności); w przypadku ogólnym wynik ten, nazywany twierdzeniem Lagrange'a, wymaga znajomości pojęcia warstwy grupy względem jej podgrupy.
opisane w wyżej („kryterium bycia grupą skończoną”) sugerują ogólną regułę, iż rząd podgrupy dzieli rząd grupy – w istocie jest ona prawdziwa: rozumowanie w przypadku skończonym wymaga jedynie znajomości pojęć grupy i funkcji (można go znaleźć w rząd: Własności); w przypadku ogólnym wynik ten, nazywany twierdzeniem Lagrange'a, wymaga znajomości pojęcia warstwy grupy względem jej podgrupy.
- Rodzaje podgrup
- Niech
 będzie dowolną grupą; zbiór
będzie dowolną grupą; zbiór  elementów grupy
elementów grupy  przemiennych z ustalonym jej elementem
przemiennych z ustalonym jej elementem  tworzy podgrupę nazywaną centralizatorem elementu
tworzy podgrupę nazywaną centralizatorem elementu  ; podobnie zbiór
; podobnie zbiór  elementów grupy
elementów grupy  które są przemienne z dowolnym jej elementem, tworzy podgrupę nazywaną centrum grupy
które są przemienne z dowolnym jej elementem, tworzy podgrupę nazywaną centrum grupy  .
.
- Dla dwóch elementów
 dowolnej grupy
dowolnej grupy  element = xyx^ -1y^ -1" src="//upload.wikimedia.org/math/e/1/c/e1c2337dddc53e2173d0eac91a17eb9b.png"/> nazywa się ich komutatorem; przy czym = e" src="//upload.wikimedia.org/math/b/b/e/bbe88e9bdbe1fa1095f3319ef8d352db.png"/> wtedy i tylko wtedy, gdy
element = xyx^ -1y^ -1" src="//upload.wikimedia.org/math/e/1/c/e1c2337dddc53e2173d0eac91a17eb9b.png"/> nazywa się ich komutatorem; przy czym = e" src="//upload.wikimedia.org/math/b/b/e/bbe88e9bdbe1fa1095f3319ef8d352db.png"/> wtedy i tylko wtedy, gdy  są przemienne, tzn.
są przemienne, tzn.  Dla „wysoce nieprzemiennych” grup (tzw. grup doskonałych) może się zdarzyć, że żaden z komutatorów nie będzie elementem neutralnym, skąd podzbiór wszystkich komutatorów grupy nie musi tworzyć podgrupy; problem ten można obejść biorąc „najmniejszą” grupę zawierającą wszystkie komutatory, tj. podgrupę przez nie generowaną (zob. Przykłady): dla danych dwóch podzbiorów
Dla „wysoce nieprzemiennych” grup (tzw. grup doskonałych) może się zdarzyć, że żaden z komutatorów nie będzie elementem neutralnym, skąd podzbiór wszystkich komutatorów grupy nie musi tworzyć podgrupy; problem ten można obejść biorąc „najmniejszą” grupę zawierającą wszystkie komutatory, tj. podgrupę przez nie generowaną (zob. Przykłady): dla danych dwóch podzbiorów  grupy
grupy  ich komutantem " src="//upload.wikimedia.org/math/4/b/8/4b8b6ccdb1c8175b9ae414e87b05d363.png"/> nazywa się podgrupę w
ich komutantem " src="//upload.wikimedia.org/math/4/b/8/4b8b6ccdb1c8175b9ae414e87b05d363.png"/> nazywa się podgrupę w  generowaną przez wszystkie komutatory ," src="//upload.wikimedia.org/math/4/c/4/4c4b4c561dcf6aa24429b33517338ac4.png"/> gdzie
generowaną przez wszystkie komutatory ," src="//upload.wikimedia.org/math/4/c/4/4c4b4c561dcf6aa24429b33517338ac4.png"/> gdzie  oraz
oraz  Podgrupę " src="//upload.wikimedia.org/math/0/0/5/0054a6f26b806514c2d4862e9b852807.png"/> nazywa się komutantem lub pochodną grupy
Podgrupę " src="//upload.wikimedia.org/math/0/0/5/0054a6f26b806514c2d4862e9b852807.png"/> nazywa się komutantem lub pochodną grupy 
- Centrum i komutant są przykładami tzw. podgrup normalnych, czyli takich podgrup
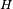 pewnej grupy
pewnej grupy  które są przemienne z dowolnym elementem
które są przemienne z dowolnym elementem  tzn. dla każdego
tzn. dla każdego  zachodzi
zachodzi  . Pojęcie podgrupy normalnej umożliwia wprowadzenie metody konstrukcji nowych grup z istniejących grup oraz ich podgrup (normalnych), mianowicie tzw. grup ilorazowych; procedura ta jest uogólnieniem uzyskiwania grup
. Pojęcie podgrupy normalnej umożliwia wprowadzenie metody konstrukcji nowych grup z istniejących grup oraz ich podgrup (normalnych), mianowicie tzw. grup ilorazowych; procedura ta jest uogólnieniem uzyskiwania grup  z mnożeniem modulo
z mnożeniem modulo  z grupy liczb całkowitych
z grupy liczb całkowitych  oraz jej podgrupy
oraz jej podgrupy  (zob. wyżej).
(zob. wyżej).
Wśród wielu przykładów grup i ich podgrup można wymienić ponadto:
- grupę wszystkich izometrii danej przestrzeni euklidesowej (z działaniem składania przekształceń) nazywaną grupą euklidesową wraz z jej podgrupami: przesunięć, odbić, czy obrotów;
- grupę wszystkich odwracalnych macierzy kwadratowych ustalonego stopnia nad danym ciałem nazywaną pełną grupą liniową z podgrupami: diagonalną, skalarną oraz specjalną grupą liniową; wśród pozostałych można wymienić podgrupy: ortogonalną, unitarną i symplektyczną;
- grupę wszystkich permutacji zbioru skończonego z działaniem ich składania nazywaną grupą symetryczną (bądź grupą permutacji) wraz z grupą alternującą tego zbioru jako jej podgrupą; twierdzenie Cayleya mówi o tym, iż każda grupa może być postrzegana jako podgrupa grupy symetrycznej: dzięki temu twierdzenia obowiązujące dla grup symetrycznych są prawdziwe również dla wszystkich grup abstrakcyjnych.
Zobacz też
- p-podgrupa (Sylowa), podgrupa torsyjna
- podgrupa Cartana, podgrupa Fittinga, podgrupa z operatorami (podgrupa stabilna)


 dlatego iloczyn elementów
dlatego iloczyn elementów  oraz
oraz  w grupie
w grupie  aby uzyskać dwuargumentowe działanie wewnętrzne na
aby uzyskać dwuargumentowe działanie wewnętrzne na  tak jak w grupie
tak jak w grupie  dla wszystkich
dla wszystkich  Innymi słowy zbiór
Innymi słowy zbiór 
 musi zachodzić
musi zachodzić  wiadomo jednak, że
wiadomo jednak, że  dla
dla  a ponieważ
a ponieważ  w ten sposób łączność działania w
w ten sposób łączność działania w  dla dowolnego
dla dowolnego  w szczególności dla elementu neutralnego
w szczególności dla elementu neutralnego  grupy
grupy  a ponieważ
a ponieważ  to z charakteryzacji elementu neutralnego grupy wynika, że
to z charakteryzacji elementu neutralnego grupy wynika, że  o ile tylko należy on do
o ile tylko należy on do 
 dla których
dla których  odczytanie tego równania w grupie
odczytanie tego równania w grupie  w postaci elementu odwrotnego do
w postaci elementu odwrotnego do  dlatego nie trzeba go szukać, lecz wystarczy sobie jedynie zapewnić, iż element odwrotny
dlatego nie trzeba go szukać, lecz wystarczy sobie jedynie zapewnić, iż element odwrotny  do
do 

 dla każdego
dla każdego 


 oraz zbiór
oraz zbiór  , nietrywialność podgrupy zaznaczana jest osobno. Jeżeli
, nietrywialność podgrupy zaznaczana jest osobno. Jeżeli 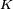 jest podgrupą w
jest podgrupą w  będzie podzbiorem liczb całkowitych
będzie podzbiorem liczb całkowitych  podzielnych przez
podzielnych przez  Zbiór
Zbiór  jest zamknięty ze względu na dodawanie i branie odwrotności, a więc
jest zamknięty ze względu na dodawanie i branie odwrotności, a więc  Analogicznie dowodzi się, że zbiór
Analogicznie dowodzi się, że zbiór  dla dowolnego
dla dowolnego  będącego liczbą naturalną jest podgrupą w
będącego liczbą naturalną jest podgrupą w  a ponadto wszystkie jej podgrupy mają tę postać.
a ponadto wszystkie jej podgrupy mają tę postać. w grupie
w grupie  niezerowych liczb wymiernych z działaniem mnożenia (iloczyn dowolnych dwóch niezerowych liczb wymiernych dalej jest niezerową liczbą wymierną i podobnie odwrotność niezerowej liczby wymiernej jest niezerową liczbą wymierną), co wynika wprost z własności iloczynu i odwrotności liczb wymiernych: jeśli
niezerowych liczb wymiernych z działaniem mnożenia (iloczyn dowolnych dwóch niezerowych liczb wymiernych dalej jest niezerową liczbą wymierną i podobnie odwrotność niezerowej liczby wymiernej jest niezerową liczbą wymierną), co wynika wprost z własności iloczynu i odwrotności liczb wymiernych: jeśli  to
to  oraz
oraz  podobne obserwacje dotyczą liczb rzeczywistych
podobne obserwacje dotyczą liczb rzeczywistych  (należy wyżej zastąpić
(należy wyżej zastąpić  znakiem
znakiem  są podgrupami w
są podgrupami w  również jest podgrupą w
również jest podgrupą w  gdyż
gdyż  oraz
oraz  ponadto jeżeli
ponadto jeżeli  to
to  i
i  skąd
skąd  i
i  a więc
a więc  dodatkowo z
dodatkowo z  wynika
wynika  i
i  a więc
a więc  i
i  co pociąga
co pociąga  stąd
stąd  rodziny
rodziny  podgrup grupy
podgrup grupy  również jest podgrupą w
również jest podgrupą w  oznacza zbiór wszystkich wzajemnie jednoznacznych odwzorowań przedziału jednostkowego " src="//upload.wikimedia.org/math/0/8/8/088246d70e0c47595fc9931fcdb11d4c.png"/>liczb rzeczywistych; tworzy on grupę ze względu na składanie odwzorowań (zob. grupa: Przykłady). Zbiór
oznacza zbiór wszystkich wzajemnie jednoznacznych odwzorowań przedziału jednostkowego " src="//upload.wikimedia.org/math/0/8/8/088246d70e0c47595fc9931fcdb11d4c.png"/>liczb rzeczywistych; tworzy on grupę ze względu na składanie odwzorowań (zob. grupa: Przykłady). Zbiór  jest podgrupą w
jest podgrupą w 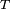 jest niepusty, gdyż należy do niego odwzorowanie tożsamościowe
jest niepusty, gdyż należy do niego odwzorowanie tożsamościowe  dane wzorem
dane wzorem  dla którego zachodzi
dla którego zachodzi 
 to
to  oraz
oraz  co oznacza
co oznacza  a więc
a więc 
 to
to  a zatem
a zatem  stąd
stąd  tzn.
tzn.  czyli
czyli 
 grupy
grupy  wraz z mnożeniem modulo
wraz z mnożeniem modulo  przy czym
przy czym  oznacza redukcję liczby całkowitej
oznacza redukcję liczby całkowitej  modulo
modulo  (tzn. resztę z dzielenia
(tzn. resztę z dzielenia 
 jest zamknięty ze względu na mnożenie. Skoro
jest zamknięty ze względu na mnożenie. Skoro  Byłaby to prawda, gdyby
Byłaby to prawda, gdyby  ); jest ona jednak grupą ze względu na dodawanie, co (jak się okazuje) jest zupełnie czymś innym – aby poprawnie zastosować wspomniane kryterium, należy się więc najpierw upewnić, że nadzbiór tworzy grupę.
); jest ona jednak grupą ze względu na dodawanie, co (jak się okazuje) jest zupełnie czymś innym – aby poprawnie zastosować wspomniane kryterium, należy się więc najpierw upewnić, że nadzbiór tworzy grupę. co wynika z własności arytmetyki modularnej); ponadto
co wynika z własności arytmetyki modularnej); ponadto  oraz
oraz  dla wszystkich
dla wszystkich  (z powyższych rozważań lub własności arytmetyki modularnej), skąd
(z powyższych rozważań lub własności arytmetyki modularnej), skąd  jest elementem neutralnym w
jest elementem neutralnym w  każdy element
każdy element 


 oraz
oraz  Korzystając z kryterium bycia podgrupą skończoną można się przekonać, iż podzbiory
Korzystając z kryterium bycia podgrupą skończoną można się przekonać, iż podzbiory 

 są nietrywialnymi podgrupami właściwymi w
są nietrywialnymi podgrupami właściwymi w  gdyż są one zamknięte ze względu na mnożenie (są to jedyne tego rodzaju podgrupy w tej grupie). Podgrupy w
gdyż są one zamknięte ze względu na mnożenie (są to jedyne tego rodzaju podgrupy w tej grupie). Podgrupy w  które są dzielnikami rzędu
które są dzielnikami rzędu  grupy
grupy 
 tworzy podgrupę grupy
tworzy podgrupę grupy  niezerowych liczb zespolonych względem mnożenia na podstawie kryterium bycia podgrupą skończoną, gdyż jest zamknięta na branie iloczynów. To samo kryterium mówi, że
niezerowych liczb zespolonych względem mnożenia na podstawie kryterium bycia podgrupą skończoną, gdyż jest zamknięta na branie iloczynów. To samo kryterium mówi, że  jest podgrupą w
jest podgrupą w  Ponadto grupa ta nie ma innych nietrywialnych podgrup właściwych, gdyż jeśli podgrupa ta zawierałaby
Ponadto grupa ta nie ma innych nietrywialnych podgrup właściwych, gdyż jeśli podgrupa ta zawierałaby  lub
lub  to musiałaby także zawierać
to musiałaby także zawierać  lub
lub  czyli tworzyłaby wtedy całą grupę
czyli tworzyłaby wtedy całą grupę  ma dokładnie trzy podgrupy: jedną rzędu
ma dokładnie trzy podgrupy: jedną rzędu  jedną rzędu
jedną rzędu  i jedną rzędu
i jedną rzędu  grupy
grupy  jest podzbiorem dodatnich liczb całkowitych (które można utożsamiać z liczbami naturalnymi
jest podzbiorem dodatnich liczb całkowitych (które można utożsamiać z liczbami naturalnymi  ), to mimo iż
), to mimo iż 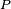 jest zamknięty na to działanie, to nie tworzy on podgrupy, gdyż brak w tym zbiorze elementu neutralnego dodawania (
jest zamknięty na to działanie, to nie tworzy on podgrupy, gdyż brak w tym zbiorze elementu neutralnego dodawania ( ); rozpatrywanie
); rozpatrywanie  (podobnie jak poprzedni przykład) narusza warunek należenia odwrotności (tu: elementu przeciwnego). Grupa
(podobnie jak poprzedni przykład) narusza warunek należenia odwrotności (tu: elementu przeciwnego). Grupa  podgrup
podgrup  bądź
bądź  tzn.
tzn.  lub
lub  czy też
czy też  albo
albo  wynika to z nieco ogólniejszej obserwacji: jeżeli
wynika to z nieco ogólniejszej obserwacji: jeżeli  to
to  lub
lub  (być może w obu z nich). Oznacza to, że nie istnieje grupa, która byłaby sumą mnogościową dwóch swoich nietrywialnych podgrup właściwych; mimo to istnieje grupa, dla której suma jej trzech różnych nietrywialnych podgrup właściwych tworzy w niej podgrupę. Twierdzenie Tomkinsona mówi, iż nie istnieje grupa, którą można zapisać w postaci sumy mnogościowej dokładnie siedmiu jej nietrywialnych podgrup właściwych, z kolei twierdzenie Skorzy stanowi o tym, że jeśli grupa jest sumą trzech nietrywialnych podgrup właściwych, to są one indeksu dwa, a części wspólne dowolnych dwóch z tych trzech podgrup są równe.
(być może w obu z nich). Oznacza to, że nie istnieje grupa, która byłaby sumą mnogościową dwóch swoich nietrywialnych podgrup właściwych; mimo to istnieje grupa, dla której suma jej trzech różnych nietrywialnych podgrup właściwych tworzy w niej podgrupę. Twierdzenie Tomkinsona mówi, iż nie istnieje grupa, którą można zapisać w postaci sumy mnogościowej dokładnie siedmiu jej nietrywialnych podgrup właściwych, z kolei twierdzenie Skorzy stanowi o tym, że jeśli grupa jest sumą trzech nietrywialnych podgrup właściwych, to są one indeksu dwa, a części wspólne dowolnych dwóch z tych trzech podgrup są równe. można scharakteryzować jako najmniejszą (w sensie zawierania) podgrupę zawierającą wszystkie elementy zbioru
można scharakteryzować jako najmniejszą (w sensie zawierania) podgrupę zawierającą wszystkie elementy zbioru  tj. część wspólną wszystkich podgrup zawierających zbiór
tj. część wspólną wszystkich podgrup zawierających zbiór  Podgrupę generowaną przez jednoelementowy podzbiór
Podgrupę generowaną przez jednoelementowy podzbiór  grupy
grupy  zaś sam element
zaś sam element  elementów grupy
elementów grupy  tworzy podgrupę nazywaną centralizatorem elementu
tworzy podgrupę nazywaną centralizatorem elementu  elementów grupy
elementów grupy  dowolnej grupy
dowolnej grupy  Dla „wysoce nieprzemiennych” grup (tzw. grup doskonałych) może się zdarzyć, że żaden z komutatorów nie będzie elementem neutralnym, skąd podzbiór wszystkich komutatorów grupy nie musi tworzyć podgrupy; problem ten można obejść biorąc „najmniejszą” grupę zawierającą wszystkie komutatory, tj. podgrupę przez nie generowaną (zob. Przykłady): dla danych dwóch podzbiorów
Dla „wysoce nieprzemiennych” grup (tzw. grup doskonałych) może się zdarzyć, że żaden z komutatorów nie będzie elementem neutralnym, skąd podzbiór wszystkich komutatorów grupy nie musi tworzyć podgrupy; problem ten można obejść biorąc „najmniejszą” grupę zawierającą wszystkie komutatory, tj. podgrupę przez nie generowaną (zob. Przykłady): dla danych dwóch podzbiorów  grupy
grupy  oraz
oraz  Podgrupę " src="//upload.wikimedia.org/math/0/0/5/0054a6f26b806514c2d4862e9b852807.png"/> nazywa się komutantem lub pochodną grupy
Podgrupę " src="//upload.wikimedia.org/math/0/0/5/0054a6f26b806514c2d4862e9b852807.png"/> nazywa się komutantem lub pochodną grupy  tzn. dla każdego
tzn. dla każdego  . Pojęcie podgrupy normalnej umożliwia wprowadzenie metody konstrukcji nowych grup z istniejących grup oraz ich podgrup (normalnych), mianowicie tzw. grup ilorazowych; procedura ta jest uogólnieniem uzyskiwania grup
. Pojęcie podgrupy normalnej umożliwia wprowadzenie metody konstrukcji nowych grup z istniejących grup oraz ich podgrup (normalnych), mianowicie tzw. grup ilorazowych; procedura ta jest uogólnieniem uzyskiwania grup  z mnożeniem modulo
z mnożeniem modulo  (zob. wyżej).
(zob. wyżej).